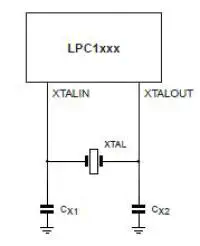
Clocks

Requirements

Layout

• Crystal are as close as possible to the device
• Crystal trace width is at least 12 mils
• There is a ground ring around crystals

Design

Compute Crystal capacitors

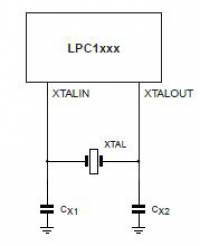
The following formula may be used to calculate a parallel resonant crystal’s external load capacitors:
$$ C_L = \frac{C_{X1} \times C_{X2}}{C_{X1} + C_{X2}} + C_{stray} $$

where :
\( C_L = \) the crystal load capacitance
\( C_{stray} = \) the stray capacitance in the oscillator circuit, which will normally be in the 2pF to 5pF range.

Assuming that \( C_{X1} = C_{X2} \) then the equation becomes:
$$ C_{X1} = 2 \times ( C_L - C_{stray} ) $$

It is difficult to know exactly what the stray capacitance is, but if you find the oscillation frequency is too high, the load capacitor values can be increased. If the frequency is too low, the load capacitors can be decreased.
The device data sheet may also define a maximum crystal series resistance \( R_s \).